Asymmetric Key Encryption Explained: A Clear Guide for Beginners
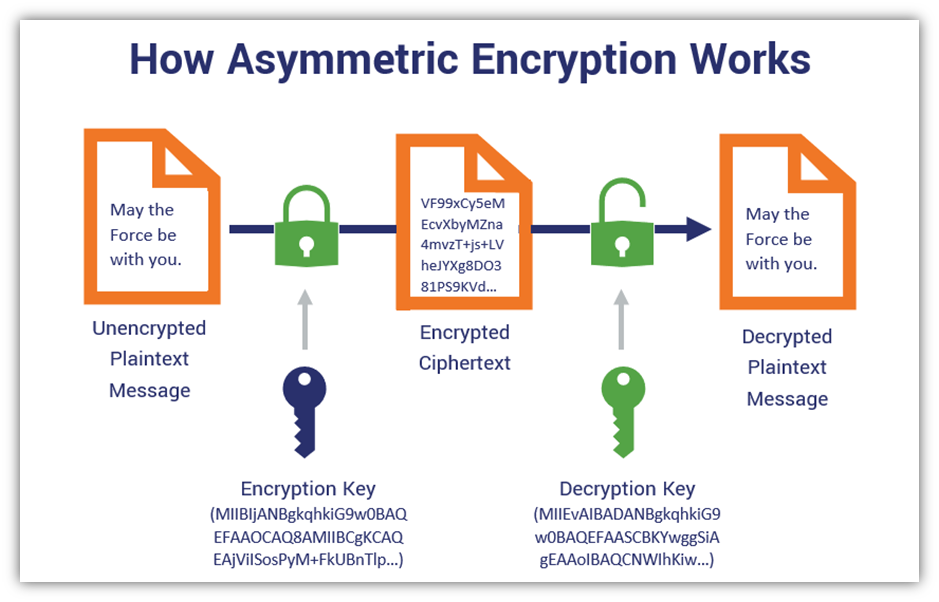
Unlike traditional encryption methods that rely on a single shared key, asymmetric key encryption employs a sophisticated dual-key system that eliminates many security vulnerabilities inherent in earlier approaches. Understanding this technology is crucial for anyone working in IT, cybersecurity, or simply wanting to comprehend how their personal data stays protected online.
What Makes Asymmetric Encryption Different?
Traditional symmetric encryption requires both parties to share the same secret key, creating a significant challenge: how do you securely distribute that key without compromising the entire system? This fundamental problem plagued cryptographers for decades until the groundbreaking work of Whitfield Diffie and Martin Hellman in the 1970s.
Asymmetric encryption solves this key distribution problem by using two keys instead of one. These keys work as a mathematically linked pair, where data encrypted with one key can only be decrypted with its corresponding partner. This elegant solution eliminates the need for secure key exchange channels while maintaining robust security.
The beauty of this system lies in its asymmetry – hence the name. The two keys perform different functions and can be safely separated. One key, called the public key, can be freely shared with anyone who wants to send you encrypted messages. The other key, the private key, must be kept absolutely secret and secure.
How the Key Pair System Works
When you generate an asymmetric key pair, sophisticated mathematical algorithms create two keys that share a unique mathematical relationship. This relationship ensures that:
- Data encrypted with the public key can only be decrypted with the corresponding private key
- Data encrypted with the private key can only be decrypted with the corresponding public key
- It’s computationally infeasible to derive one key from the other
This mathematical foundation relies on complex problems that are easy to compute in one direction but extremely difficult to reverse without additional information. Most asymmetric encryption algorithms base their security on problems like integer factorization or discrete logarithms.
The key generation process involves selecting large prime numbers and performing mathematical operations that create the key pair. The resulting keys are typically much larger than symmetric encryption keys – often 2048 bits or more – because the mathematical problems underlying asymmetric encryption require larger key spaces to maintain equivalent security levels.
Primary Use Cases and Applications
Secure Communication
The most common application involves encrypting messages for secure transmission. When Alice wants to send Bob a confidential message, she uses Bob’s public key to encrypt the data. Only Bob, possessing the corresponding private key, can decrypt and read the message. This process ensures that even if the encrypted message is intercepted during transmission, unauthorized parties cannot access its contents.
Digital Signatures
Asymmetric encryption also enables digital signatures, which provide authentication and non-repudiation. When signing a document digitally, you encrypt a hash of the document with your private key. Recipients can then use your public key to decrypt this signature, verifying both that the document came from you and that it hasn’t been tampered with since signing.
Key Exchange Protocols
Many systems use asymmetric encryption to establish secure channels for symmetric encryption. Since symmetric encryption is much faster for large amounts of data, a common approach involves using asymmetric encryption to securely exchange symmetric keys, then switching to symmetric encryption for the actual data transmission.
Common Asymmetric Encryption Algorithms
Several asymmetric encryption algorithms have gained widespread adoption, each with distinct characteristics and use cases:
RSA (Rivest-Shamir-Adleman)
RSA remains the most widely recognized asymmetric encryption algorithm. Developed in 1977, it bases its security on the difficulty of factoring large composite numbers. RSA’s versatility allows it to handle both encryption and digital signatures, making it a popular choice for many applications.
The algorithm works by selecting two large prime numbers, multiplying them together, and using this product as part of both keys. The security relies on the fact that while multiplying two large primes is straightforward, factoring their product back into the original primes is computationally intensive without additional information.
Elliptic Curve Cryptography (ECC)
ECC offers equivalent security to RSA with significantly smaller key sizes, making it ideal for mobile devices and embedded systems where computational resources are limited. Instead of relying on integer factorization, ECC bases its security on the discrete logarithm problem over elliptic curves.
This algorithm’s efficiency stems from the mathematical properties of elliptic curves, which provide exponential security growth relative to key size. A 256-bit ECC key offers roughly equivalent security to a 3072-bit RSA key, resulting in faster computations and reduced storage requirements.
Digital Signature Algorithm (DSA)
DSA was specifically designed for digital signatures rather than general encryption. It uses a different mathematical approach based on discrete logarithms in finite fields. While less versatile than RSA, DSA often provides better performance for signature operations.
Real-World Implementation Example
Consider a practical asymmetric key encryption example involving an online banking system. When you log into your bank’s website, several asymmetric encryption processes occur:
First, your browser requests the bank’s digital certificate, which contains the bank’s public key. Your browser uses this public key to encrypt a randomly generated symmetric key, which it sends to the bank’s server. The bank’s server uses its private key to decrypt this symmetric key.
Once both parties possess the same symmetric key, they switch to symmetric encryption for the actual data transmission. This hybrid approach combines asymmetric encryption’s security benefits with symmetric encryption’s speed advantages.
Throughout this process, asymmetric encryption ensures that even if someone intercepts the initial key exchange, they cannot access the symmetric key without the bank’s private key. This layered security approach protects your financial transactions from eavesdropping and manipulation.
Security Considerations and Best Practices
Key Management
Proper key management is crucial for maintaining asymmetric encryption security. Private keys must be stored securely, often using hardware security modules or encrypted key stores. Regular key rotation helps limit the impact of potential compromises.
Public keys, while shareable, should be distributed through trusted channels to prevent man-in-the-middle attacks. Digital certificates signed by trusted certificate authorities provide one solution to this authentication challenge.
Key Length Selection
Choosing appropriate key lengths involves balancing security requirements with performance considerations. As computational power increases, previously secure key lengths may become vulnerable to brute-force attacks. Current best practices recommend minimum key lengths of 2048 bits for RSA and 256 bits for ECC.
Implementation Vulnerabilities
Even mathematically sound algorithms can be compromised by poor implementation. Common vulnerabilities include weak random number generation, side-channel attacks, and timing analysis. Using well-tested cryptographic libraries rather than implementing algorithms from scratch helps mitigate these risks.
Performance and Scalability Factors
Asymmetric encryption operations are significantly slower than symmetric encryption, typically 100-1000 times slower depending on the algorithm and key size. This performance difference influences how and when asymmetric encryption is used in practice.
For large-scale systems, hybrid encryption approaches become essential. These systems use asymmetric encryption only for key exchange and authentication, relying on symmetric encryption for bulk data processing. This strategy provides strong security while maintaining acceptable performance levels.
The computational overhead also affects mobile and IoT devices with limited processing power. In these environments, choosing efficient algorithms like ECC becomes crucial for maintaining usability while preserving security.
Future Developments and Challenges
Quantum computing poses a significant threat to current asymmetric encryption methods. Quantum algorithms like Shor’s algorithm could potentially break RSA and ECC encryption in polynomial time, rendering these methods obsolete.
This threat has sparked development of post-quantum cryptography algorithms designed to resist quantum attacks. These new approaches typically rely on different mathematical problems, such as lattice-based cryptography or hash-based signatures.
The transition to post-quantum cryptography will require careful planning and gradual implementation to maintain security while ensuring compatibility with existing systems. Organizations must begin preparing for this transition now, even though practical quantum computers capable of breaking current encryption may still be years away.
Conclusion
Asymmetric key encryption represents one of the most significant advances in modern cryptography, enabling secure communication and digital commerce on a global scale. Its elegant solution to the key distribution problem has made possible everything from secure email to online banking to digital contracts.
Understanding the fundamental principles, common algorithms, and practical applications of asymmetric encryption is essential for anyone involved in cybersecurity or digital communications. As technology continues evolving, particularly with the emergence of quantum computing threats, staying informed about developments in asymmetric encryption remains crucial for maintaining digital security.
While the mathematical complexity underlying these systems may seem daunting, the practical benefits are clear: asymmetric encryption provides the foundation for trust in our digital world, enabling secure interactions between parties who have never met and may never meet in person.